 |
| ||||
Home Page
F.A.Qs
Statistical Charts
Past Contests
Scheduled Contests
Award Contest
| ||||||||||
| Online Judge | Problem Set | Authors | Online Contests | User | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Web Board Home Page F.A.Qs Statistical Charts | Current Contest Past Contests Scheduled Contests Award Contest | |||||||||
|
Language: Supersquare
Description Let number A be a precise square if there exists natural number B such that B*B = A. 2n-digit number without leading zeroes is called a supersquare if it is a precise square and both n-digit numbers which are formed from its n first digits and its n last digits are precise squares. The second n-digit number dndn-1…d1 formed from n last digits may have leading zeroes but must not be equal zero. 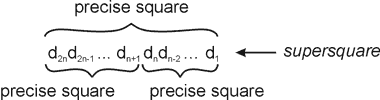 You need to write a program which constructs a 2n-digit number which is supersquare. Input The input contains several test cases. The first line contains the number of test cases T (1 ≤ T ≤ 10). Each of the next T lines describes one test case and contains an integer number n (1 ≤ n ≤ 500). Output The output consists of T lines, one line per each test case. Each line contains 2n-digit supersquare number. If several solutions are possible only one of them should be given. When it is impossible to construct 2n-digit supersquare, the line must contain NO SUPERSQUARE POSSIBLE phrase. Sample Input 2 1 2 Sample Output 49 1681 Source Northeastern Europe 2005, Western Subregion | ||||||||||
[Submit] [Go Back] [Status] [Discuss]
All Rights Reserved 2003-2013 Ying Fuchen,Xu Pengcheng,Xie Di
Any problem, Please Contact Administrator