 |
| ||||
Home Page
F.A.Qs
Statistical Charts
Past Contests
Scheduled Contests
Award Contest
| ||||||||||
| Online Judge | Problem Set | Authors | Online Contests | User | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Web Board Home Page F.A.Qs Statistical Charts | Current Contest Past Contests Scheduled Contests Award Contest | |||||||||
|
Language: Manhattan Wiring
Description There is a rectangular area containing n × m cells. Two cells are marked with “2”, and another two with “3”. Some cells are occupied by obstacles. You should connect the two “2”s and also the two “3”s with non-intersecting lines. Lines can run only vertically or horizontally connecting centers of cells without obstacles. Lines cannot run on a cell with an obstacle. Only one line can run on a cell at most once. Hence, a line cannot intersect with the other line, nor with itself. Under these constraints, the total length of the two lines should be minimized. The length of a line is defined as the number of cell borders it passes. In particular, a line connecting cells sharing their border has length 1. Fig. 1(a) shows an example setting. Fig. 1(b) shows two lines satisfying the constraints above with minimum total length 18. 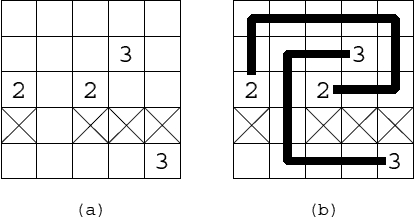 Figure 1: An example of setting and its solution Input The input consists of multiple datasets, each in the following format.
n is the number of rows which satisfies 2 ≤ n ≤ 9. m is the number of columns which satisfies 2 ≤ m ≤ 9. Each rowi is a sequence of m digits separated by a space. The digits mean the following.
The end of the input is indicated with a line containing two zeros separated by a space. Output For each dataset, one line containing the minimum total length of the two lines should be output. If there is no pair of lines satisfying the requirement, answer “ Sample Input 5 5 0 0 0 0 0 0 0 0 3 0 2 0 2 0 0 1 0 1 1 1 0 0 0 0 3 2 3 2 2 0 0 3 3 6 5 2 0 0 0 0 0 3 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 2 3 0 5 9 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 2 0 0 0 0 0 2 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 9 9 3 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 3 9 9 0 0 0 1 0 0 0 0 0 0 2 0 1 0 0 0 0 3 0 0 0 1 0 0 0 0 2 0 0 0 1 0 0 0 0 3 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 9 9 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 3 2 0 0 Sample Output 18 2 17 12 0 52 43 Source | ||||||||||||||
[Submit] [Go Back] [Status] [Discuss]
All Rights Reserved 2003-2013 Ying Fuchen,Xu Pengcheng,Xie Di
Any problem, Please Contact Administrator