Closed polyline (with possible self-intersections) partitions a plane into a number of regions. One of the regions is unbounded -- it is an exterior of the polyline. All the bounded regions together with the polyline itself form an interior of the polyline (shaded in the picture below). The border of the interior (bold line in the picture) is a polyline as well. This polyline has the same interior as the original one.
Your task is to find the border of the interior of the given polyline.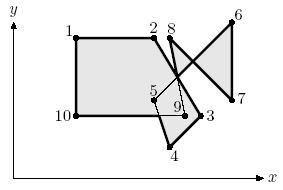

To guarantee the uniqueness (up to the starting point) of the polyline representing the border we require that the following conditions are satisfied for it:

• it has no self-intersections, although may have self-touchings;
  
• no adjacent vertices of the border coincide;
  
• no adjacent edges of the border are collinear;
  
• when traversing the border, its interior is always to the left of its edges.

The first line of the input file contains an integer number n (3 <= n <= 100) -- the number of vertices in the original polyline. Following n lines contain two integer numbers xi and yi on a line (0 <= xi, yi <= 100) -- coordinates of the vertices. All vertices are different and no vertex lies on an edge between two other vertices. Adjacent edges of the polyline are not collinear.

Write to the output file an integer number m -- the number of vertices of the border. Then write m lines with coordinates of the vertices. Coordinates must be precise up to 4 digits after the decimal point.

10
4 9
9 9
12 4
10 2
9 5
14 10
14 5
10 9
11 4
4 4

13
9.3333 4
10 2
12 4
10.5 6.5
11.5 7.5
14 5
14 10
11.5 7.5
10 9
10.5 6.5
9 9
4 9
4 4