 |
| ||||
Home Page
F.A.Qs
Statistical Charts
Past Contests
Scheduled Contests
Award Contest
| ||||||||||
| Online Judge | Problem Set | Authors | Online Contests | User | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Web Board Home Page F.A.Qs Statistical Charts | Current Contest Past Contests Scheduled Contests Award Contest | |||||||||
|
Language: Disks
Description Consider N floating point numbers N representing the radii of N disks. We fix a disk in the xOy system, if we position it at a positive coordinate x (big enough), tangential to the 0x axis and above it and after that we push it to 0y until it becomes tangent to 0y or to the first disk that it meets on the way. In the configuration that results by fixing in order all the given disks, some of them can be considered as being dispensible, because, if we eliminate them, the total width of the configuration is the same, which means that there is no disk that can be moved to the left.
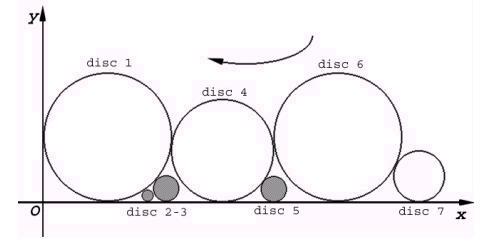 Identify all the indispensible disks for a given configuration (in the configuration from above; the gray disks are dispensible). Input The input has the following structure:
Output The output will have the following structure:
Sample Input 7 4 0.1 0.5 3 0.5 4 1 Sample Output 3 2 3 5 Source |
[Submit] [Go Back] [Status] [Discuss]
All Rights Reserved 2003-2013 Ying Fuchen,Xu Pengcheng,Xie Di
Any problem, Please Contact Administrator