3960 -- Binary Operation

Language:

Binary Operation

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 241		Accepted: 69

Description

Consider a binary operation $\odot$ defined on digits 0 to 9. $\odot$ : {0, 1, ..., 9} × {0, 1, ..., 9} $\to$ {0, 1, ..., 9}, such that 0 $\odot$ 0 = 0.
A binary operation $\otimes$ is a generalization of $\odot$ to the set of non-negative integers, $\otimes$ : $\mathbb{Z}$ ₀₊ × $\mathbb{Z}$ ₀₊ $\to$ $\mathbb{Z}$ ₀₊. The result of a $\otimes$ b is defined in the following way: if one of the numbers a and b has fewer digits than the other in decimal notation, then append leading zeroes to it, so that the numbers are of the same length;
then apply the operation 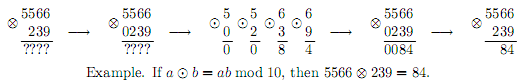$\odot$ digit-wise to the corresponding digits of a and b.

Let us define $\otimes$ to be left-associative, that is, a $\otimes$ b $\otimes$ c is to be interpreted as (a $\otimes$ b) $\otimes$ c.
Given a binary operation $\odot$ and two non-negative integers a and b, calculate the value of a $\otimes$ (a + 1) $\otimes$ (a + 2) $\otimes$ ... $\otimes$ (b - 1) $\otimes$ b.

Input

The first ten lines of the input file contain the description of the binary operation $\odot$ . The i-th line of the input file contains a space-separated list of ten digits - the j-th digit in this list is equal to (i - 1) $\odot$ (j - 1).
The first digit in the first line is always 0.
The eleventh line of the input file contains two non-negative integers a and b (0 <= a <= b <= 10¹⁸).

Output

Output a single number – the value of a $\otimes$ (a + 1) $\otimes$ (a + 2) $\otimes$ ... $\otimes$ (b - 1) $\otimes$ b without extra leading zeroes.

Sample Input

0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 0
2 3 4 5 6 7 8 9 0 1
3 4 5 6 7 8 9 0 1 2
4 5 6 7 8 9 0 1 2 3
5 6 7 8 9 0 1 2 3 4
6 7 8 9 0 1 2 3 4 5
7 8 9 0 1 2 3 4 5 6
8 9 0 1 2 3 4 5 6 7
9 0 1 2 3 4 5 6 7 8
0 10

Sample Output

Source

Northeastern Europe 2010