3929 -- Timer

Language:

Timer

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 341		Accepted: 90

Description

Recently, some archaeologists discovered an ancient relic on a small island in the Pacific Ocean. In the relic, they found an interesting cone shaped container with transparent bottom. The container lay on the horizontal ground with its central axis parallel to the ground. Just beside the container, they found a manual telling them something about the container. The container was a timer for a special ceremony. Ancient people filled it all with water before the ceremony, and when the ceremony began, they pulled out the plug in the small hole on the tip of the cone to let the water out. There was a horizontal line called “sacred line” carved on the bottom of the cone, and when the water level hit that line, they pushed the plug back and ended the ceremony. But the archaeologists could not found the sacred line on that cone. In order to sell the timer at a good prize, the archaeologists wanted to recover that very important line. By the manual they figured out how much water flew out when the ceremony ended, but they don't know what to do next, so they come to you for help.

They measures the height of the cone, and the diameter of the bottom, you should tell them the sacred line's height above the ground.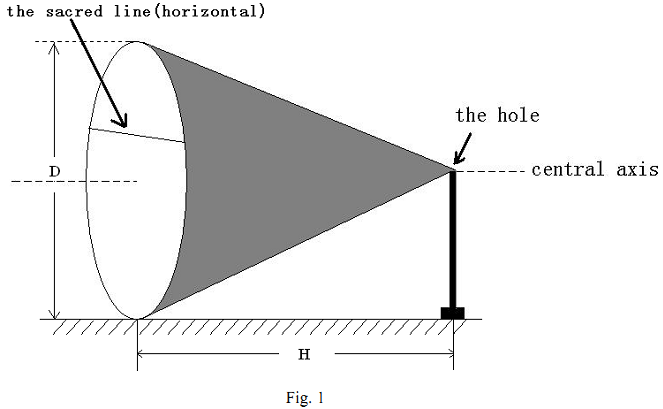

Input

The first line of the input contains an integer T(1<=T<=20), indicating the number of test cases. Each line after that is a test case. It contains three real numbers, H, D(1<=H,D<=1000) and V, indicating the height and bottom diameter of the timer, and the volume of water that flew out during the ceremony. That volume is guaranteed to be less than half volume of the container.

Output

For each test case, output one line containing the height of the sacred line above the ground. You should round off the answers to the 5th decimal place. (For example, rounding off 4.000005 equals to 4.00001 and rounding off 4.000004 equals to 4.00000)

Sample Input

2 
5.0 10.0 0.0 
5.0 10.0 65.4498

Sample Output

10.00000 
5.00000

Hint

Here are some formulas you may need. Please notice that in these formulas, Log means log_e or ln.

$\int\sqrt{x^2-a^2}dx=\frac{1}{2}x\sqrt{x^2-a^2}-\frac{1}{2}a^2Log\left[x+\sqrt{x^2-a^2}\right]+C$
$\int\sqrt{x^2+a^2}dx=\frac{1}{2}x\sqrt{x^2+a^2}+\frac{1}{2}a^2Log\left[x+\sqrt{x^2+a^2}\right]+C$
$\int\sqrt{a^2-x^2}dx=\frac{1}{2}\left(x\sqrt{a^2-x^2}+a^2ArcTan\left[\frac{x}{\sqrt{a^2-x^2}}\right]\right)+C$
$\int Log\left[a+\sqrt{a^2-x^2}\right]dx=aArcTan\left[\frac{x}{\sqrt{a^2-x^2}}\right]+x\left(-1+Log\left[a+\sqrt{a^2-x^2}\right]\right)+C$
$\int xLog\left[a+\sqrt{a^2-x^2}\right]dx=\frac{1}{4}\left(a^2-x^2-2a\sqrt{a^2-x^2}+2x^2Log\left[a+\sqrt{a^2-x^2}\right]\right)+C$
$\int x^2Log\left[a+\sqrt{a^2-x^2}\right]dx=\frac{1}{18}\left(-2x^3-3ax\sqrt{a^2-x^2}+3a^3ArcTan\left[\frac{x}{\sqrt{a^2-x^2}}\right]+6x^3Log\left[a+\sqrt{a^2-x^2}\right]\right)+C$

Source

Beijing 2008