For a tree, which nodes and edges are all weighted, the ratio of it is calculated according to the following equation.



Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.

Input contains multiple test cases. The first line of each test case contains two integers n (2<=n<=15) and m (2<=m<=n), which stands for the number of nodes in the graph and the number of nodes in the minimal ratio tree. Two zeros end the input. The next line contains n numbers which stand for the weight of each node. The following n lines contain a diagonally symmetrical n×n connectivity matrix with each element shows the weight of the edge connecting one node with another. Of course, the diagonal will be all 0, since there is no edge connecting a node with itself.

All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].

The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.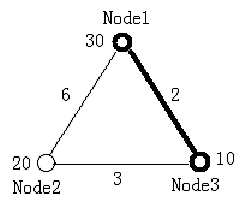

For each test case output one line contains a sequence of the m nodes which constructs the minimal ratio tree. Nodes should be arranged in ascending order. If there are several such sequences, pick the one which has the smallest node number; if there's a tie, look at the second smallest node number, etc. Please note that the nodes are numbered from 1.

3 2 
30 20 10 
0 6 2 
6 0 3 
2 3 0 
2 2 
1 1 
0 2 
2 0 
0 0

1 3 
1 2