3377 -- Ferry Lanes

Language:

Ferry Lanes

Time Limit: 2000MS		Memory Limit: 131072K
Total Submissions: 6554		Accepted: 1292

Description

Arthur lives in a small city which is partitioned into two districts, the northern and the southern, by a river flowing through. The northern and southern districts are connected by N + 1 bidirectional ferry lanes, numbered 0 to N from west to east. Each ferry lane connects two docks in separate sides of the river. No two lanes share the same dock or cross each other.

Today Arthur needs to deliver a package from one dock to another. He knows the sailing time of each ferry lane and the time cost by walking from one dock to an adjacent one along the river bank. Arthur wants to know what is the minimum time his delivery will cost.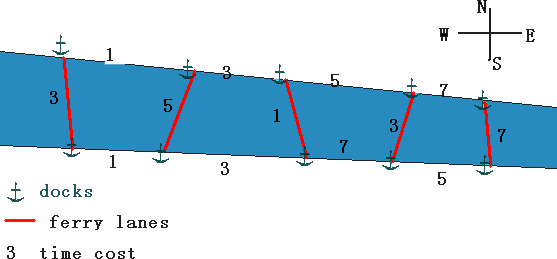

Input

The input consists of several test cases. The first line of each consists an integer N ( 1 ≤ N ≤ 1,000,000). The second line consists of two pairs of integers describing the starting and finishing docks, where the first of each pair represents the district (0 means northern and 1 means southern) and the second represents the lane number. The third line contains N integers describing the time cost by walking between two adjacent docks on the northern bank from lane₀ to lane_N. The fourth line contains N + 1 integers describing the sailing time of each ferry lane. The last line contains N integers describing the time cost by walking between two adjacent docks on the southern bank from lane₀ to lane_N. N = 0 indicates the end of input.

Output

For each test cases output one line contains the minimum time. You may assume the answer fits in a signed 64-bit integer.

Sample Input

Sample Output

Source

POJ Monthly--2007.09.09, Dagger