3221 -- Diamond Puzzle

Language:

Diamond Puzzle

Time Limit: 2000MS		Memory Limit: 131072K
Total Submissions: 1641		Accepted: 901

Description

A diamond puzzle is played on a tessellated hexagon like the one shown in Figure 1 below. And in this problem the faces produced by the tessellation are identified as they are numbered in the same figure. If two faces share a side, they are called neighboring faces. Thus, even-numbered faces have three neighboring faces, while odd-numbered faces have only two. At any point during the play of the puzzle, six of the seven faces hold a unique digit ranging from 1 to 6, and the other one is empty. A move in the puzzle is to move a digit from one face to a neighboring empty one.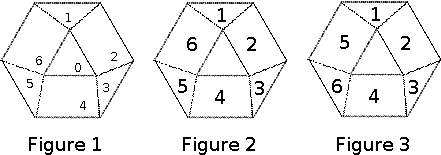

Starting from any configuration, some series of moves can always make the puzzle look identical to either one shown in Figures 2 and 3. Your task is to calculate the minimum number of moves to make it become the one in Figure 2.

Input

The input contains multiple test cases. The first contains an integer N (0 ≤ N ≤ 5,040), the number of test cases. Then follow N lines, each with a permutation of {0, 1, 2, 3, 4, 5, 6} describing a starting configuration of the puzzle. The ith digit in the permutation is the one in the face numbered i − 1. A zero means the face is empty.

Output

For each test cases, output the minimum number of moves the configuration takes to reach the one shown in Figure 2. If this is impossible, just output “-1” and nothing else.

Sample Input

Sample Output

10
-1
0

Source

PKU Local 2007 (POJ Monthly--2007.04.28), wenxichang