 |
| ||||
Home Page
F.A.Qs
Statistical Charts
Past Contests
Scheduled Contests
Award Contest
| ||||||||||
| Online Judge | Problem Set | Authors | Online Contests | User | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Web Board Home Page F.A.Qs Statistical Charts | Current Contest Past Contests Scheduled Contests Award Contest | |||||||||
|
Language: Triangular N-Queens Problem
Description A “queen” piece on a triangular array of cells, N cells on a side, can attack any cell on a file parallel to one of the sides containing the queen’s cell. For example, in the array in Figure 1, a queen on the black cell, attacks all of the shaded cells. The Triangular N-Queens Problem of size N, is to find a maximal set of queen positions in a triangular array with N cells on a side so that no queen is attacking any other queen. For example, the black cells in Figure 2 give a maximal set of queen positions in a size 6 array. It turns out that a size N array always has floor((2 * N + 1) ⁄ 3) as the maximal number of non-attacking queen positions. 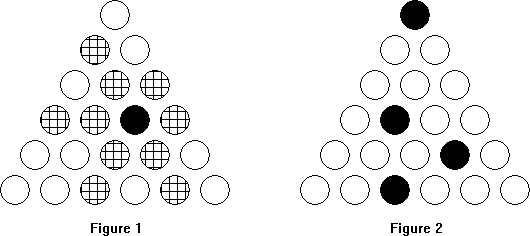 Write a program, which, given the size, N, of the triangular array, finds a maximal set of non-attacking queen positions on the array (floor((2 * N + 1) ⁄ 3) of them). Input The input begins with a line containing an integer value specifying the number of datasets that follow, C (1 ≤ C ≤ 1000). Each dataset consists of a single line containing a single integer N, (1 ≤ N ≤ 1000), which is the size of the triangular array. Output The first output line for each problem gives the problem number starting at 1, a single space, the input size, a single space and the number of queen positions. Following the first line will be the queen positions, 8 positions per line except perhaps for the last line of positions. Each position has the format open bracket (‘[’), row number starting with 1, a comma, the position from the left within the row starting at 1 and a close bracket (‘]’). Positions within a line are separated by a single space. For example, the queen positions in Figure 2 are [1,1] [4,2] [5,4] [6,3]. The lines of position values are followed by a single blank line. Sample Input 6 3 6 9 10 14 18 Sample Output 1 3 2 [1,1] [3,2] 2 6 4 [3,1] [4,3] [5,5] [6,2] 3 9 6 [4,1] [5,3] [6,5] [7,7] [8,2] [9,4] 4 10 7 [4,1] [5,3] [6,5] [7,7] [8,2] [9,4] [10,6] 5 14 9 [6,1] [7,3] [8,5] [9,7] [10,9] [11,11] [12,2] [13,4] [14,6] 6 18 12 [7,1] [8,3] [9,5] [10,7] [11,9] [12,11] [13,13] [14,2] [15,4] [16,6] [17,8] [18,10] Hint Notes
Source | ||||||||||
[Submit] [Go Back] [Status] [Discuss]
All Rights Reserved 2003-2013 Ying Fuchen,Xu Pengcheng,Xie Di
Any problem, Please Contact Administrator