 |
| ||||
Home Page
F.A.Qs
Statistical Charts
Past Contests
Scheduled Contests
Award Contest
| ||||||||||
| Online Judge | Problem Set | Authors | Online Contests | User | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Web Board Home Page F.A.Qs Statistical Charts | Current Contest Past Contests Scheduled Contests Award Contest | |||||||||
|
Language: Cake Cutting
Description You are given a rectangular cake of integral dimensions w × h. Your goal is to divide this cake into m rectangular pieces of integral dimensions such that the area of the largest piece is minimal. Each cut must be a straight line parallel to one of the sides of the original cake and must divide a piece of cake into two new pieces of positive area. Note that since a cut divides only a single piece, exactly m − 1 cuts are needed. If w = 4, h = 4, and m = 4, then the following cuts minimize the area of the largest piece: 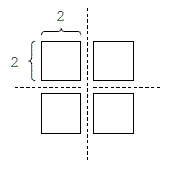 However, if w = 4, h = 4, and m = 3, then the following cuts are optimal: 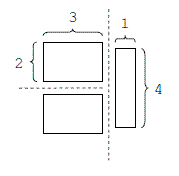 Input The input test file will contain multiple test cases, each of which consists of three integers w, h, m separated by a single space, with 1 ≤ w, h, m ≤ 20 and m ≤ wh. The end-of-file is marked by a test case with w = h = m = 0 and should not be processed. Output For each test case, write a single line with a positive integer indicating the area of the largest piece. Sample Input 4 4 4 4 4 3 0 0 0 Sample Output 4 6 Source |
[Submit] [Go Back] [Status] [Discuss]
All Rights Reserved 2003-2013 Ying Fuchen,Xu Pengcheng,Xie Di
Any problem, Please Contact Administrator