 |
| ||||
Home Page
F.A.Qs
Statistical Charts
Past Contests
Scheduled Contests
Award Contest
| ||||||||||
| Online Judge | Problem Set | Authors | Online Contests | User | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Web Board Home Page F.A.Qs Statistical Charts | Current Contest Past Contests Scheduled Contests Award Contest | |||||||||
|
Language: Diophantus of Alexandria
Description Diophantus of Alexandria was an Egypt mathematician living in Alexandria. He was one of the first mathematicians to study equations where variables were restricted to integral values. In honor of him, these equations are commonly called Diophantine equations. One of the most famous Diophantine equation is xn + yn = zn. Fermat suggested that for n > 2, there are no solutions with positive integral values for x, y and z. A proof of this theorem (called Fermat’s last theorem) was found only recently by Andrew Wiles. Consider the following Diophantine equation:
Diophantus is interested in the following question: for a given n, how many distinct solutions (i. e., solutions satisfying x ≤ y) does equation (1) have? For example, for n = 4, there are exactly three distinct solutions: 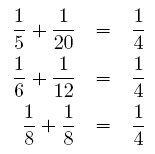 Clearly, enumerating these solutions can become tedious for bigger values of n. Can you help Diophantus compute the number of distinct solutions for big values of n quickly? Input The first line contains the number of scenarios. Each scenario consists of one line containing a single number n (1 ≤ n ≤ 109). Output The output for every scenario begins with a line containing “Scenario #i:”, where i is the number of the scenario starting at 1. Next, print a single line with the number of distinct solutions of equation (1) for the given value of n. Terminate each scenario with a blank line. Sample Input 2 4 1260 Sample Output Scenario #1: 3 Scenario #2: 113 Source TUD Programming Contest 2006, Darmstadt, Germany |
[Submit] [Go Back] [Status] [Discuss]
All Rights Reserved 2003-2013 Ying Fuchen,Xu Pengcheng,Xie Di
Any problem, Please Contact Administrator