 |
| ||||
Home Page
F.A.Qs
Statistical Charts
Past Contests
Scheduled Contests
Award Contest
| ||||||||||
| Online Judge | Problem Set | Authors | Online Contests | User | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Web Board Home Page F.A.Qs Statistical Charts | Current Contest Past Contests Scheduled Contests Award Contest | |||||||||
|
Language: Light Up
Description Light Up is a puzzle set in a rectangular board divided in smaller squares. Some squares in the board are ``empty'' (white squares the figure below), some squares are ``barriers'' (dark squares in the figure below). A barrier square may have an integer number i associated to it (0 <= i <= 4).
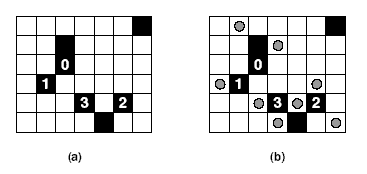
Figure 2: (a) Puzzle with 6 rows, 7 columns and 7 barriers; (b) a solution to the puzzle. In this puzzle the goal is to ``light up'' all the empty squares by placing lamps in some of them (lamps are depicted as circles in the figure). Each lamp illuminates the square it is on, plus all squares in line with it, horizontally or vertically, up to a barrier square or the board end. A winning configuration satisfies the following conditions:
You must write a program to determine the smallest number of lamps that are needed to reach a winning configuration. Input The input contains several test cases. The first line of a test case contains two integers N, M indicating respectively the number of rows and the number of columns of the board (1 <= N <= 7, 1 <= M <= 7). The second line contains one integer B indicating the number of barrier squares (0 <= B <= N × M). Each of the next B lines describe a barrier, containing three integers R, C and K, representing respectively the row number (1 <= R <= N), the column number (1 <= C <= M) and the barrier number (-1 <= K <= 4); K = -1 means the barrier is unnumbered. The end of input is indicated by N = M = 0. Output For each test case in the input your program must produce one line of output, containing either an integer indicating the smallest number of lamps needed to reach a winning configuration, in case such a configuration exists, or the words `No solution'. Sample Input 2 2 0 2 2 1 2 2 1 6 7 7 2 3 -1 3 3 0 4 2 1 5 4 3 5 6 2 1 7 -1 6 5 -1 0 0 Sample Output 2 No solution 8 Source |
[Submit] [Go Back] [Status] [Discuss]
All Rights Reserved 2003-2013 Ying Fuchen,Xu Pengcheng,Xie Di
Any problem, Please Contact Administrator