 |
| ||||
Home Page
F.A.Qs
Statistical Charts
Past Contests
Scheduled Contests
Award Contest
| ||||||||||
| Online Judge | Problem Set | Authors | Online Contests | User | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Web Board Home Page F.A.Qs Statistical Charts | Current Contest Past Contests Scheduled Contests Award Contest | |||||||||
|
Language: Silver Matrix
Description If a matrix satisfies the following conditions, we call it a silver matrix.
1. The dimensions of the matrix are n * n. 2. All its elements belong to the set S = {1, 2, 3, …, 2n - 1}. 3. For every integer i (1 <= i <= n), all elements in the i-th row and i-th column make the set {1, 2, 3, …, 2n - 1}. For example, the following 4 * 4 matrix is a silver matrix: 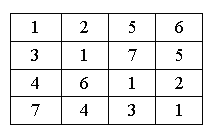 It is proved that silver matrix with size 2K * 2K always exists. And it is your job to find a silver matrix with size 2K * 2K. Input The input contains only an integer K (1 <= K <= 9). Output You may output any matrix with size 2K * 2K. To output a 2K * 2K matrix, you should output 2K lines, and in each line output 2K integers. Sample Input 2 Sample Output 1 2 5 6 3 1 7 5 4 6 1 2 7 4 3 1 Source POJ Monthly--2006.06.25, Lei Tao | ||||||||||
[Submit] [Go Back] [Status] [Discuss]
All Rights Reserved 2003-2013 Ying Fuchen,Xu Pengcheng,Xie Di
Any problem, Please Contact Administrator