 |
| ||||
Home Page
F.A.Qs
Statistical Charts
Past Contests
Scheduled Contests
Award Contest
| ||||||||||
| Online Judge | Problem Set | Authors | Online Contests | User | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Web Board Home Page F.A.Qs Statistical Charts | Current Contest Past Contests Scheduled Contests Award Contest | |||||||||
|
Language: Packing Dominoes
Description A domino is a 2 x 1 oblong comprising two squares, each square marked with a set of "pips" denoting a non-negative integer. A blank square denotes the number 0 (zero).
In a standard " double-K " set of dominoes, each pair of integers in the range 0...K occurs on one domino. In other words, the dominoes are numbered: (0, 0),(0, 1),...(0, K),(1, 1),...(1, K),(2, 2),...,(K, K) Given a set of dominoes and a rectangular area of width w and height h , write a program to pack that entire set of dominoes into that area subject to the limitation that, whenever two dominoes touch one another either horizontally or vertically, the numbers on the touching squares must be identical. Note that the area might not be completely covered, and, space permitting, some dominoes might not touch any others. Input Input will consist of one or more lines, each containing 3 positive integers. The first integer, K , indicates the size of the set of dominoes - a "double-K set" as described above. The remaining integers, w and h , indicate the size of the area in which the dominoes should be placed, measured in units the same size as one of the constituent squares of a domino. The end of input will be signaled by a non-positive K value. Output For each line of input, print one line containing the values K(K<=3) , w , and h (w,h<=12), as defined above, followed either by a line with the string ``No packing is possible" or by a report consisting of (K+1)(K+2)/2 lines, each line describing one domino, ordered as described above in the definition of a ``doubleK " set.
Each line of that report will contain 6 integers d1 d2 x1 y1 x2 y2 where d1 and d2 are the numbers on that domino, (x1, y1) is the coordinates of the number d1 in the packed layout, and (x2, y2) is the coordinates of number d2 . Coordinates are specified as integers with (0,0) denoting the lower-left corner of the packing area. If multiple packings are possible, any packing meeting the criteria outlined above will be accepted. Sample Input 1 5 3 3 5 2 -1 0 0 Sample Output 1 5 3 0 0 0 0 0 1 0 1 1 0 2 0 1 1 3 0 3 1 3 5 2 No packing is possible Hint Note: This output corresponds to the packing shown here and is only one of many possible correct responses.
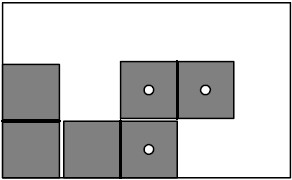 Source | ||||||||||
[Submit] [Go Back] [Status] [Discuss]
All Rights Reserved 2003-2013 Ying Fuchen,Xu Pengcheng,Xie Di
Any problem, Please Contact Administrator