A set of n 1-dimensional items have to be packed in identical bins. All bins have exactly the same length l and each item i has length li<=l . We look for a minimal number of bins q such that

• each bin contains at most 2 items,
  
• each item is packed in one of the q bins,
  
• the sum of the lengths of the items packed in a bin does not exceed l .

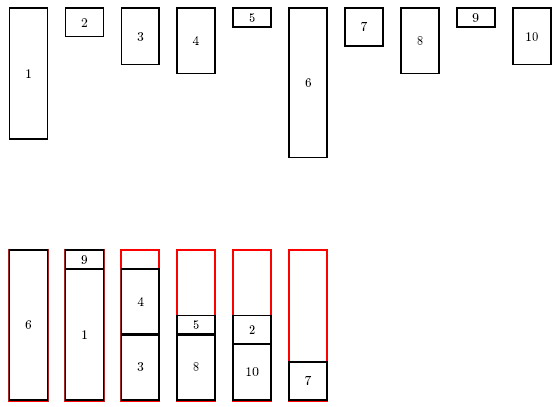
You are requested, given the integer values n , l , l1 , ..., ln , to compute the optimal number of bins q .

The first line of the input contains the number of items n (1<=n<=10⁵) . The second line contains one integer that corresponds to the bin length l<=10000 . We then have n lines containing one integer value that represents the length of the items.

Your program has to write the minimal number of bins required to pack all items.

10
80
70
15
30
35
10
80
20
35
10
30

6

The sample instance and an optimal solution is shown in the figure below. Items are numbered from 1 to 10 according to the input order.