The background knowledge of this problem comes from "Similarity of necklaces". Do not worry. I will bring you all the information you need.

The little cat thinks about the problem he met again, and turns that problem into a fair new one, by putting N * (N + 1) / 2 elements into a linear list, with M = N * (N + 1) / 2 elements:



(The above table denotes Table and Pairs in description of after converting)

One more array named "Multi" appears here. Suppose Pairs and Multi are given, the little cat's purpose is to determine an array Table with M integers that obey:



(this condition is similar with the condition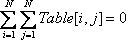



that appears in the problem "Similarity of necklaces") and make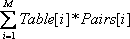



as large as possible. What is more, we must have Low[i] <= Table[i] <= Up[i] for any 1 <= i <= M. Here Low and Up are two more arrays with M integers given to you.

The input contains a number of test cases. Each of the following blocks denotes a single test case. A test case starts by an integer M (1 <= M <= 200) and M lines followed. The i-th line followed contains four integers: Pairs[i], Multi[i], Low[i], Up[i].

Restrictions: -25 <= Low[i] < Up[i] <= 25, 0 <= Pairs[i] <= 100000, 1 <= Multi[i] <= 20. From the input given, you may assume that there is always a solution.

For each test case, output a single line with a single number, which is the larges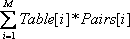t

10
7 1 1 10
0 2 -10 10
2 2 -10 10
0 2 -10 10
0 1 1 10
0 2 -10 10
0 2 -10 10
0 1 1 10
0 2 -10 10
0 1 1 10

10
0 1 1 10
2 2 -10 10
2 2 -10 10
2 2 -10 10
0 1 1 10
2 2 -10 10
2 2 -10 10
0 1 1 10
2 2 -10 10
0 1 1 10

90
-4

POJ Monthly--2006.01.22,Zeyuan Zhu