Advanced Control Mechanisms (ACM) produces sophisticated electronic locks and security devices.
The company's most recent invention is a panel of illuminated buttons in r rows and c columns. The buttons are numbered left-to-right, top-to-bottom, starting at 1 in the upper-left corner. Each button has two states: lit and unlit. Initially, all buttons are unlit. Pressing a button switches the state of some buttons from lit to unlit (or vice-versa) according to a 3x3 pattern. Pressing a button on a panel applies the pattern centered on that button. To unlock the panel, the buttons must be pressed in such a way so as to light all of them.

For example, consider the following pattern where pressing a button switches the state of the button pressed, as well as the button above and the buttons to the upper and lower left.

If we use this patern on a 2x3 panel, then pressing buttons 2, 5, and 6 will light all the buttons. If pressed in that order, the state changes of the panel are: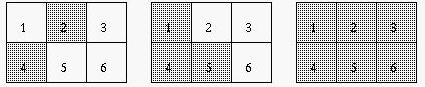

Each input case will begin with the number of rows and columns on the panel, 1 <= r,c <= 5 alone on a line. The next three lines describe how pressing a button will affect the nearby lights. This description consists of a 3x3 character grid, where the character "*" indicates that the light in that position switches state (from lit to unlit or from unlit to lit) while "." means its state remains unchanged.
Input ends with 0 0 alone on a line.

For each input case, output "Case #" followed by the number of the case. If there is no way to turn on all the lights, print "Impossible." If it is possible to turn on the lights, output the buttons to be pressed in increasing order, separated by single space. Output the answer that requires the fewest number of buttons possible to be pressed.

2 3
**.
.*.
*..
4 5
.*.
***
.*.
2 2
...
.**
...
4 3
*.*
...
..*
0 0

Case #1
2 5 6
Case #2
2 3 4 7 9 12 14 17 18 19 
Case #3
1 3 
Case #4
Impossible.