 |
| ||||
Home Page
F.A.Qs
Statistical Charts
Past Contests
Scheduled Contests
Award Contest
| ||||||||||
| Online Judge | Problem Set | Authors | Online Contests | User | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Web Board Home Page F.A.Qs Statistical Charts | Current Contest Past Contests Scheduled Contests Award Contest | |||||||||
|
Language: Greatest Common Subtree
Description We say tree T1 is a top-bottom subtree of tree T if
1. T1 is a tree and its nodes and edges are respectively the subsets of T’s nodes and edges, and 2. w is node of tree T1 but not the root of T, then w’s parent is also in tree T1. 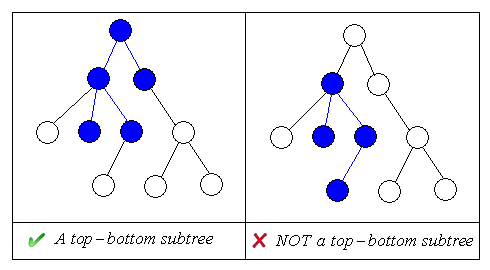 We say two rooted unordered trees are isomorphic if 1. a tree with a single node (the root) is only isomorphic to a tree with a single node; 2. two trees with roots A and B, none of which is a single-node tree, are isomorphic iff there is a 1-1 correspondence between the subtrees of A and the subtrees of B such that corresponding subtrees are isomorphic. 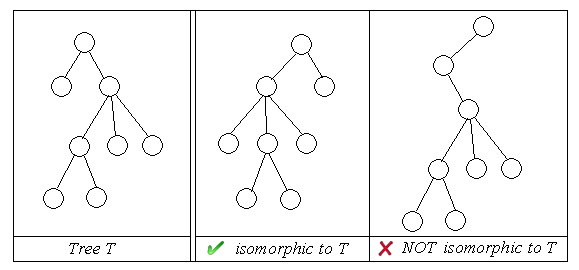 Given two rooted unordered trees, your task is to find out their top-bottom subtrees respectively which are isomorphic, and maximize the number of nodes of the subtrees, i.e., the Greatest Common Subtree. 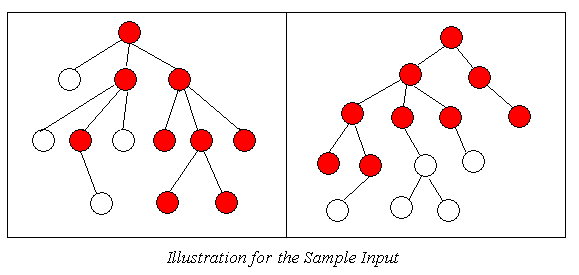 Input There are several test cases in the input file. The first line of each case contains two integers: n and m, representing the number of nodes of the first tree and the second. 1<=n, m<=50. n-1 lines follow, with two integers each, indicating the label of the node and its parent in the first tree. Then m-1 lines follow, with two integers each line, indicating the label of the node and its parent in the second tree. Nodes are labeled from 1 and the node labeled 1 is always the root.There is an empty line after each case. Output For each test case, output the number of nodes of the Greatest Common Subtree in a line. Sample Input 13 14 2 1 3 1 4 1 5 3 6 3 7 3 8 4 9 4 10 4 11 6 12 9 13 9 2 1 3 1 4 2 5 2 6 2 7 3 8 4 9 4 10 5 11 6 12 9 13 10 14 10 Sample Output 9 Source POJ Contest,Author:kinfkong@ZSU |
[Submit] [Go Back] [Status] [Discuss]
All Rights Reserved 2003-2013 Ying Fuchen,Xu Pengcheng,Xie Di
Any problem, Please Contact Administrator