To save money you are considering renting a small cube van to transport your belongings to the Big City. The interior of the van is a rectangular box with width w, height h, and length l. The box has a sliding door that lifts but only to height H. That is, there is an immovable overhang of height H-h at the top of the door.
You have a large rectangular box that you wish to load on the truck. Can you get it on the truck subject to the following constraints:

• The box must fit through the door, tilting it forward or sideways (but not both) as necessary (see figure below).
  
• The box must be placed with one side flat against the floor.
  
• The box must be placed with one side flat against the front wall.
  
• The door must close once the box is in place.

You may assume there are no obstructions (such as a ceiling or the ground) outside the truck that might interfere with loading.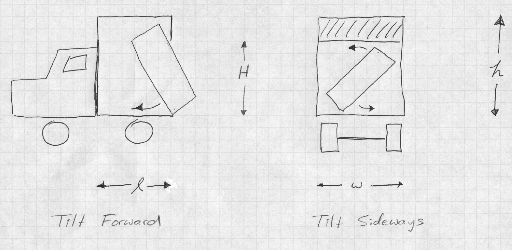

There are several test cases, each represented by two lines of input. The first line of each contains 4 integers: w, h, l, H. The next line contains 3 integers - the dimensions of the box.

For each test case, print "The box goes on the truck." if it is possible to load the box on the truck; otherwise print "The box will not go on the truck." You may assume that you start with an empty truck for each test case.

8 8 12 7
8 12 8
8 8 12 7
7 12 8
8 8 12 7
1 7 13
100 200 99 190
100 195 30

The box will not go on the truck.
The box goes on the truck.
The box will not go on the truck.
The box goes on the truck.