A simple dartboard consists of a flat, circular piece of cork with concentric rings drawn on it. Darts are thrown at the board by players in an attempt to hit the center of the dartboard (the Bullseye). The region between each pair of rings (or the center and the first ring) represents a certain point value. The closer the region is to the center of the dartboard, the more points the region is worth, as shown in the diagram below:

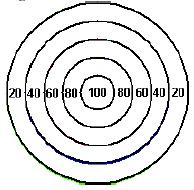Ring radii are at 3", 6", 9", 12" and 15" (the Bullseye has a diameter of 6"). A game of Simple Darts between two players is played as follows. The first player throws 3 darts at the board. A score is computed by adding up the point values of each region that a dart lands in. The darts are removed. The second player throws 3 darts at the board; the score for player two is computed the same way as it is for player one. The player with the higher score wins.

For this problem, you are to write a program that computes the scores for two players, and determine who, if anyone, wins the game. If a dart lands exactly on a ring (region boundary), the higher point value is awarded. Any dart outside the outer ring receives no points. For the purposes of this problem, you can assume that a dart has an infinitely fine point and can not land paritially on a ring; it is either on the ring or it is not on the ring. Standard double precision floating point operations will be should be used.

Input consists of 1 or more datasets. A dataset is a line with 12 double-precision values separated by spaces. Each pair of values represents the X and Y distances respectively of a dart from the center of the board in inches. (the center is located at X = 0, Y = 0. The range of values are: -20.0<=X, Y<=20.0. Player one's darts are represented by the first 3 pairs of values, and player two's by the last 3 pairs of values. Input is terminated by the first value of a dataset being -100.

For each dataset, print a line of the form:

SCORE: N to M, PLAYER P WINS. 

Or:

SCORE: N to M, TIE. 

N is player one's score, and M is player two's score. P is either 1 or 2 depending on which player wins. All values are non-negative integers.

Formula

Recall: r² = x² + y² where r is the radius, and (x, y) are the coordinates of a point on the circle.

-9 0 0 -4.5 -2 2 9 0 0 4.5 2 -2
-19.0 19.0 0 0 0 0 3 3 6 6 12 12
-100 0 0 0 0 0 0 0 0 0 0 0

SCORE: 240 to 240, TIE.
SCORE: 200 to 140, PLAYER 1 WINS.