Background
For hundreds of years fire departments all over the world have been using water for their fight against the fire. Unfortunately, one cannot always find enough water right where the fire is burning. Accordingly, the fire departments are equipped with lots of pumps and pipes to transport the water to where it is needed.Setting up the system of pumps and pipes might not be such an easy task, as there are several restrictions one has to take care of.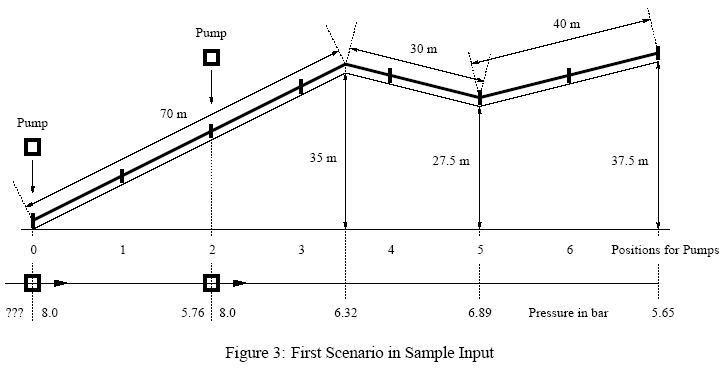

The Problem
Let us assume that only one type of pipes is used for the transportation of water, namely pipes with a diameter of 75 millimeters and a length of 20 meters. Depending on the quantity of water that is pumped through the tubes, there is a loss of pressure per meter according to the following table:

flow (f) in liters per minute              loss of pressure in millibar per meter

             200                                             1

             400                                             3

             600                                             6

             800                                            10

            1000                                            15

            1200                                            20

The pressure is also affected by the profile of the landscape, more precisely the pressure changes by 1 bar every 10 meters of vertical distance, decreasing for pipes running uphill and increasing for pipes running downhill. Pumps need an input pressure of at least 2 bar and produce a constant output pressure of 8 bar, but they cannot be used to reduce pressure. Pipes do not resist a pressure higher than 12 bar, and for a constant flow a pressure of at least 2 bar is needed at all points. At the end of the line, the pressure must be at least 5 bar and at most 8 bar to permit effective fire fighting. There is always a pump at the beginning of the line of pipes (position 0). Other pumps can be placed wherever two pipes are attached to each other but not at the end.
Write a program to find the least number of pumps necessary, and their positions. If several solutions with the least number of pumps exist, prefer the ones where pumps are placed closer to the beginning of the line (carrying these pumps is no fun. . . ).

The first line contains the number of scenarios.
For each scenario, you are first given an integer f ∈ {200, 400, 600, 800, 1000, 1200} on a line by itself,indicating the desired flow in liters per minute. The next line contains two integers n and m, separated by a single blank, where 1 <= n <= 20 is the number of pipes to be used, and 1 <= m <= 400 is the number of segments with a constant slope.
The followingmlines describe thesemsegments, each containing integers l and s, separated by a single blank, where l > 0 is the length in meters and s is the slope measured in per cent (s = 10 means that pipes of a length of 100 meters ascend by 10 meters, s = -50 means they descend 50 meters; -100 <= s <= 100).
It is guaranteed that the m given lengths add up to n times 20 meters.

The output for each scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. The next line contains the number of pumps in the optimal solution (if it exists),followed by a colon ":" and a single blank, and the positions of the pumps separated by commas "," and no blanks. If no placement of the pumps satisfies the given criteria, print a line containing "no solution" instead. Finish the output of each scenario with an additional blank line.

2
600
7 3
70 50
30 -25
40 25
1000
8 4
20 0
80 -100
20 10
40 30

Scenario #1:
2: 0,2

Scenario #2:
no solution

TUD Programming Contest 2002, Darmstadt, Germany