Joseph Fourier was a great mathematician and physicist and is well known for his mathematic series. Among all the nineteen children in his family, Joseph was the youngest and the smartest. He began to show his interest in mathematics when he was very young. After he grew up, he often corresponded with C. Bonard (a professor of mathematics at Auxerre) by exchanging letters.

In one letter written to Bonard, Fourier asked a question: how to draw 17 lines on a plane to make exactly 101 crossings, where each crossing belongs to exactly two lines. Obviously, this is an easy problem, and Figure-1 is a solution that satisfies his requirement. Now the problem for you is a universal one. Can we draw N lines on a plane to make exactly M crossings, where each crossing belongs to exactly two lines? If we can, how many pieces, at most, can these lines cut the plane into?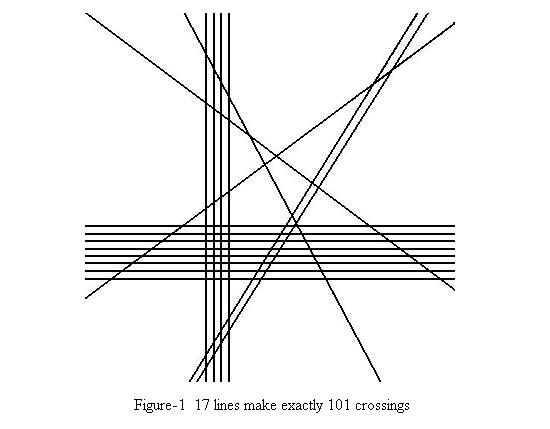

The input may have several sets of test data. Each set is one line containing two integers N and M (1 <= N <= 100, 0 <= M <= 10000), separated by a space. The test data is followed by a line containing two zeros, which indicates the end of input and should not be processed as a set of data.

Output one line for each set of input in the following format:

Case i: N lines cannot make exactly M crossings.

if the drawing of these lines is impossible;

or:

Case i: N lines with exactly M crossings can cut the plane into K pieces at most.

Note: Even if N or M equals to one, you should use the words "lines" and "crossings" in your output.

4 3
4 6
4 2
5 11
17 101
0 0

Case 1: 4 lines with exactly 3 crossings can cut the plane into 8 pieces at most.
Case 2: 4 lines with exactly 6 crossings can cut the plane into 11 pieces at most.
Case 3: 4 lines cannot make exactly 2 crossings.
Case 4: 5 lines cannot make exactly 11 crossings.
Case 5: 17 lines with exactly 101 crossings can cut the plane into 119 pieces at most.