Professor Balltazar is a big football fan. His birthday was just a couple of days before he was going to leave for the World Cup Football '98 in France, so his friends gave him as a present a dodecahedron-shaped puzzle as an entertainment while watching the boring games.
The puzzle has 12 equal pentagon sides, labelled with numbers 1 ... 12. The figure below shows the two hemispheres of the dodecahedron, together with the side labelling we will use in this problem. Hemispheres are "glued" together in such a way that the side 7 is adjacent to the sides 8, 12, 11, 2 and 6 (sides are adjacent if they share an edge). In particular, edges a and b on the left hemisphere will be glued to the edges a and b on the right hemisphere shown below.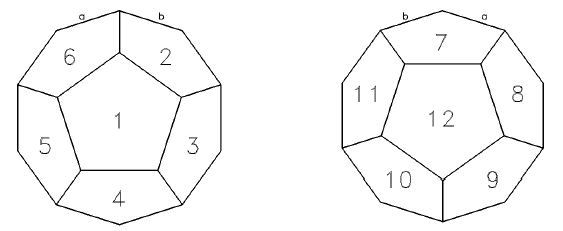

In addition to that, there are 12 pentagon-shaped tiles, also labelled from 1 to 12. Every edge on each of the tiles is marked with a number from the set {0, 1, 2}. Each tile can be placed on each of the twelve sides in any of the 5 positions obtained by rotating the tile around its centre.

To solve the puzzle, we need to put each tile on some of the twelve dodecahedron sides in some position, so that every two adjacent tiles have their common edge marked with the same number.

Help Professor Balltazar to solve the puzzle !

The input contains 12 lines. For each i, 1 <= i <= 12, the i^th line describes the i^th tile by specifying 5 numbers from the set {0, 1, 2} separated by single blank characters. This sequence shows the edge marking of the i^th tile starting from an arbitrary edge (called the ith reference edge) going in the clockwise direction.

Output should contain the description of a solved puzzle in 12 lines with 2 integers in each line. For each i, 1 <= i <= 12, the i^th line should contain integers t[i] and n[i] separated by a single blank character describing the tile and its position on the i^th side :
The i^th side will hold the tile labelled t[i].

The tile can be placed on the i^th side in five different positions. The exact position is specified by n[i], which denotes the label of the adjacent side which is in the direction of the t[i]^th reference edge (looking from the centre of the i^th side). Precisely, the t[i]^th reference edge is placed on the dodecahedron edge shared by the sides labelled i and n[i].

If the puzzle can not be solved, only number -1 should be written to the output file.

0 0 1 1 2
0 2 1 0 1
2 0 1 0 1
0 0 1 2 1
0 2 1 1 2
2 0 1 2 1
0 2 1 2 1
2 2 1 0 1
1 2 2 0 0
0 2 1 0 2
0 2 1 2 0
2 0 1 2 0

1 2
3 7
12 4
7 9
9 1
11 8
8 2
4 6
5 4
2 12
6 3
10 7