A young schoolboy would like to calculate the sum

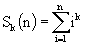
for some fixed natural k and different natural n. He observed that calculating i^k for all i (1<=i<=n) and summing up results is a too slow way to do it, because the number of required arithmetical operations increases as n increases. Fortunately, there is another method which takes only a constant number of operations regardless of n. It is possible to show that the sum S_k(n) is equal to some polynomial of degree k+1 in the variable n with rational coefficients, i.e.,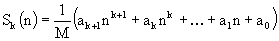

We require that integer M be positive and as small as possible. Under this condition the entire set of such numbers (i.e. M, a_k+1, a_k, ... , a₁, a₀) will be unique for the given k. You have to write a program to find such set of coefficients to help the schoolboy make his calculations quicker.

The input file contains a single integer k (1<=k<=20).

Write integer numbers M, a_k+1, a_k, ... , a₁, a₀ to the output file in the given order. Numbers should be separated by one space. Remember that you should write the answer with the smallest positive M possible.

2

6 2 3 1 0