Long, long ago there was a monster lived in Adventure Castle of Magic. One day he saw that the prince Infante Concord and his wife Princess Charm were living so sweet a life. Couldn't help becoming jealous, he used his powerful magic to turn the prince to an ugly frog. The brave and smart princess made up her mind to rescue her husband. After overcomed thousands of difficulties and challenges, she finally arrived at the Adventure Castle of Magic. When she saw her dearest handsome husband had become an ugly and awful frog by the curse of the monster, her heart almost broken. The monster gave her a very hard puzzle as a condition to exchange the prince. The princess was required to choose the right ones from some given ropes. A right rope means that the rope wouldn't make a knot by pulling up its two ends. If the princess chose all the right ones, the curse would disappear and the price would be rescued, otherwise he would be strangled to death. In order to rescue her husband, without hesitation, the princess accepted the challenge.

Here are two example ropes. Figure_1 is a right rope while Figure_2 is not a right rope:

Figure_1

The first line of the input is an integer t (1 <= t <= 20), representing the number of ropes. Each of the following lines describes a rope.

We describe the rope by pointing out the cross-point (See Figure_2). We first number all the cross-point. Then, our fingers go along the rope from one end to the other, whenever we encounter a cross-point we will record its number on the paper. If the rope goes above the point, we write down a positive number. If the rope goes under the point, we write down a negative number. In the end, we put a zero as an end sign. For example, the rope shown in Figure_2 is recorded as:

+1 -2 +3 -4 +5 -6 -7 +8 +2 -1 -10 +9 -8 -3 +4 -5 +6 +7 -9 +10 0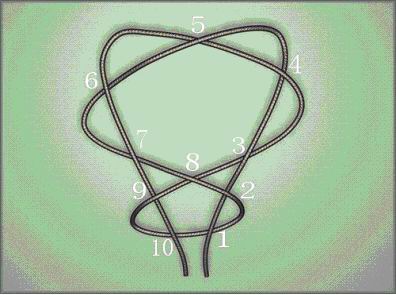

Figure_2

For each rope, output one line. If the rope will make a knot by pulling up its ends, output "Not right". Otherwise, output "Right".

3
+1 -1 0
-1 -2 -3 +1 +2 +3 0
+1 -2 +3 -4 +5 -6 -7 +8 +2 -1 -10 +9 -8 -3 +4 -5 +6 +7 -9 +10 0

Right
Right
Not right