Two points A(x1, y1, z1) and B(x2, y2, z2) are placed on the surface of parallelepiped P = {(x, y, z): 0 <= x <= L, 0 <= y <= W, 0 <= z <= H} with L*W*H dimensions (see figure). These two points can be linked with various curves lying on the surface of P. You are to find out the square of the shortest curve length.

Parallelepiped dimensions L, W, H and coordinates of the points are integers, 0 <= L,W,H <= 1000.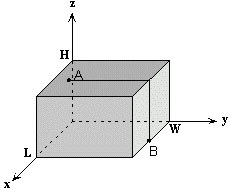

Input contains (in indicated order): L, W, H, x1, y1, z1, x2, y2, z2. The numbers are separated with spaces and end-of-line characters.

Output should contain the square of the shortest curve length between points A and B on the surface of P.

5 5 2
3 1 2
3 5 0

36