1388 -- Hinge Node Problem

In decades, people have realized the significance of data communication. Most of the designs and analysis of communication networks usually model their topologies as graphical representations because many relevant problems of networks can be solved by using graph theoretic results. As usual, a communication network is modeled by a graph that nodes and edges in a graph correspond to the communication sites and links, respectively. A network G = (N,E) consists of a set N of nodes together with a set E of edges, representing pairs of nodes. If the pairs are considered to be unordered, then we have an undirected network and the edge joining two nodes u and v is represented by (u, v). For example, Figure 3 depicts a network G which contains 10 nodes and 16 edges.

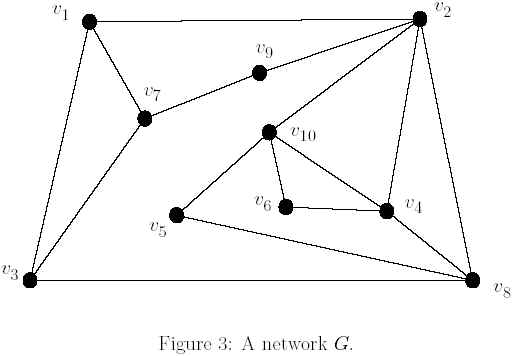In a network G, the distance between two nodes u and v, denoted by dG(u, v), is the number of edges of a shortest path from u to v in G. A sequence of vertices v1, v2, ..., vk is a path from v1 to vk of length k-1 in G provided that there is an edge between vi and vi+1 for i = 1, 2, ..., k-1. If no path exists between nodes u and v, then dG(u, v) = ∞. A path is a shortest path between nodes u and v if its length is minimum among all of the paths between u and v. A network is connected if there exists a path between any two nodes. The failure of a node w means that w and all its incident edges are removed from G, and the remaining subnetwork is denoted by G-w.A node w is called a hinge node if there exist two other nodes u and v in G such that dG-w(u, v)>dG(u, v). It means that the distance between u and v is increased after w is removed from G. Thus, a hinge node can be viewed as a critical node of the corresponding network and the failure of such a node will increase the communication cost to the remaining subnetwork. For example, we consider the network G in Figure 3. The node v2 is a hinge node since dG-v2(v8, v9)=3 > dG(v8, v9)=2. Indeed, the set of hinge nodes contained in G is {v2, v3, v4, v7, v8, v10}

Suppose that we have several networks. Each network is connected and contains at most n nodes, where 3 <= n<= 100. Assume now that you are hired to serve as a network administrator and you should analyze the communication cost. For this reason, you will be interested in finding all hinge nodes in a network. In particular, you should design a program that can efficiently calculate the total number of hinge nodes for each of the given networks.

The input file consists more than one and less than six networks (cases). Each test case starts with a positive integer n, where 3 <= n <= 100. The following n lines represents the adjacency matrix of a network G. The last case is followed by a "0" to indicate "end of input." An adjacency matrix of a network G with n nodes, denoted by A(G) = [au,v], is an n x n 0, 1-matrix such that au,v = 1 if (u, v) ∈ E, and au,v = 0 otherwise. Note that there is not any delimiter between any two elements in each line of a 0, 1-matrix. For example, the adjacency matrix of the graph in Figure 3 is shown in test case 3 of the sample input.