We can number binary trees using the following scheme:
The empty tree is numbered 0.
The single-node tree is numbered 1.
All binary trees having m nodes have numbers less than all those having m+1 nodes.
Any binary tree having m nodes with left and right subtrees L and R is numbered n such that all trees having m nodes numbered > n have either Left subtrees numbered higher than L, or A left subtree = L and a right subtree numbered higher than R.

The first 10 binary trees and tree number 20 in this sequence are shown below: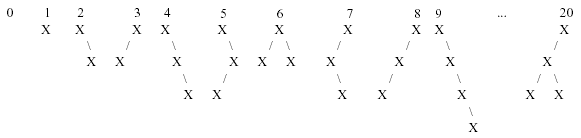

Your job for this problem is to output a binary tree when given its order number.

Input consists of multiple problem instances. Each instance consists of a single integer n, where 1 <= n <= 500,000,000. A value of n = 0 terminates input. (Note that this means you will never have to output the empty tree.)

For each problem instance, you should output one line containing the tree corresponding to the order number for that instance. To print out the tree, use the following scheme:

A tree with no children should be output as X.
A tree with left and right subtrees L and R should be output as (L')X(R'), where L' and R' are the representations of L and R.
If L is empty, just output X(R').
If R is empty, just output (L')X.

1
20
31117532
0

X
((X)X(X))X
(X(X(((X(X))X(X))X(X))))X(((X((X)X((X)X)))X)X)