Problem A: Alignments

The four alignments have to be handled separately. Possibly the most tricky point lies in the calculation of gap widths, which demands some care.

Problem B: Binomial Coefficients

The parity of C(n, k) can be determined by calculating the exponent of 2 in its factorization.

Problem C: Context-Free Language

An efficient solution is based on dynamic programming. We first decide what variables each terminal in the string can be derived from using rules of the form A → a. When we have decided information about derivation for all substrings of length not longer than k, we can next decide that for all substrings of length k + 1 by trying to divide each of them into two parts to match the rules of the form A → BC. The string belongs to the language of the grammar if and only if it can be derived from the start symbol S.

Problem D: Diamond Puzzle

The minimum numbers of steps required for every configuration of the puzzle can be precomputed by performing a (backward) breadth-first search from the final configuration and stored in a table. Rest of the job is merely table lookups.

Problem E: Edge Pairing

A simple undirected graph with an even number of edges can always have its edges grouped into incident pairs. Below is a proof by construction.

Let r be some vertex in the graph. We grow a depth-first search tree T rooted at r. Since the graph is connected, T actually spans every vertex. We then construct the pairing bottom up,  starting from the leaves. We mark all edges connecting a leave and its parent as unpaired. When working on some vertex x, we count how many unpaired edges connect x and its descendants. If the number of such edges is even, they will all be paired using x as the shared vertex, then the tree edge connecting x and its parent will be marked as unpaired; otherwise pairing fails leaving a single edge, which will be paired with that tree edge. The latter case never occurs with r. The reason is that when we work on r, all edges not connecting r and some of its descendants will have been paired, totaling to an even count. If at this moment pairing leaves a last unpaired edge, this would imply that the graph has an odd number of edges, contradicting the condition that the graph has an even number of edges.

Problem F: Football Game

Let’s first consider the simplified case where P is allowed to be anywhere on the straight line through UV.

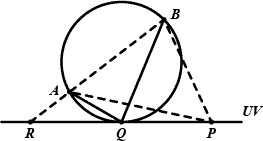
In the above figure, a circle through A and B touches UV at tangent point Q, which is to the right of R, the intersection of UV and the extension of BA. We claim that

• for any point P on the ray RQ, ∠APB ≤ ∠AQB;
• ∠APB is a convex function with respect to the position of P;
• ∠APB reaches its maximum when P coincides with Q.

These three lemmas allow the employment of the bisection method. And the method also works with the original case where the choice of P is restricted to between UV.

Additionally, the tangent point Q can also be analytically determined taking advantage of the fact that Q is the projection of O, the center of the circle, on UV. Since O is equidistant to A, B and UV, it lies on the parabolas with A and B as the foci and UV as the common directrix, and therefore is one of their intersections. Finding O from the formulæ of parabolas requires only solving a univariate quadratic equation.

Problem G: Go for Lab Cup!

Intended as the easiest one, this problem requires only a straightforward implementation of its ideas.

Problem H: Help with Intervals

Efficient representation and manipulation of the set S requires a subtle choice of data structure. Segment tree is one among possible ones. Each node in the tree stores information about membership in S of its corresponding interval, namely whether the interval completely, partially or do not belong to S and whether membership is inverted in this interval (used for quick handling of symmetric difference). Information stored in each node is carefully maintained in each operation. Finally the composition of S can be extracted from the tree.