The following is based on solutions provided by the problem setters.

以下内容以出题人提供的解答为基础。

Problem A: Who Gets the Most Candies?

This problem is a variant of the Josephus problem which can be solved with segment tree. Let P be the largest antiprime not exceeding N. The P-th child jumping out of the circle is the answer. Distribution of antiprimes is sparse. All antiprimes required for this problem can be computed in advance and hard-coded into the source.

这个问题是约瑟夫问题的一个变种，可以用线段树解决。如果不超过N的最大反素数是P，那么第P个出圈的孩子就是答案。反素数的分布很稀疏。这个题目用到的全部反素数可以提前计算出来直接写到源代码中。

Problem B: Big String

There is an algorithm whose running time does not rely on the length of the initial string. Consider the inserted characters to be inserted into gaps between successive characters of the initial string. Before each insertion, keep all previous insertions in a table ordered by their positions. To insert a character before p-th character of the current string, start from the p-th character of the initial string and walk backward to find the right position for insertion, which can be found in at most N steps. Queries can be processed in a similar way. This algorithm runs in time O(N²).

可以设计出不依赖于原始字符串长度的算法。把每个插入的字符看作被插入到初始字符串的相邻字符之间的空隙中。每次插入前，把之前插入的所有字符按顺序保存在一张表中。要在第p个字符之前插入一个字符，只需从初始字符串的第p个字符开始向前寻找，最多回退N步就可找到合适的插入位置。查询可以用类似方法处理。算法的时间复杂度是O(N²)。

Problem C: Bracelet

This is a constrained orbit-counting problem where Burnside’s lemma applies. The constraints can be represented by a directed graph. There is a edge from vertex i to vertex j if and only if beads of kind i and kind j can be stringed next to each other. Let A be the adjacency matrix. Then the answer is given by the expression below.

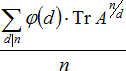
这是个有约束的轨道计数问题，可以应用Burnside引理解决。约束可以用一个有向图来表示。从顶点i到顶点j有一条边当且仅当种类i和种类j的珠子可以相邻。记邻接矩阵为A，则答案由上面的式子给出。

Problem D: Unique Solution

This problem is to determine whether there exists a unique set of M non-overlapping segments of consecutive elements of a sequence of N integers such that the sum of elements it covers is maximum. The algorithm is based on dynamic programming and recursion. First, use dynamic programming to build an M by N table of which the element in the i-th row and the j-th column is the maximum sum under the condition that the problem is limited to i segments on the first j elements and the j-th element is covered. Second, enumerate all possible last segments in the optimal set and use recursion to determine whether the set is unique.

确定一个N个元素的整数序列的最大M段和是否有唯一解。算法基于动态规划和递归。首先，用动态规划求出一张表。第i行第j列的元素表示前i个整数的最大j段和的最优解。然后，枚举最优解中的最后一段，用递归确定最优解是否唯一。

Problem E: Matrix Multiplication

Matrix multiplication won’t do for this problem. The given matrix A can be regarded as the adjacency matrix of a directed graph. Since all elements on the primary diagonal are 1’s and the dimensions are less than 2006, the graph with A²⁰⁰⁶ as its adjacency matrix is the transitive closure of the graph represented by A. The number of elements that are 1’s is equal to the number of ordered pairs of vertices (i, j) such that there exists from vertex i to vertex j.

矩阵乘法不能解决这个题目。给出的矩阵A可以看作一个有向图的邻接矩阵。由于主对角线上的元素都是1，而且矩阵的阶小于2006，所以为A²⁰⁰⁶邻接矩阵的图就是由A表示的图的传递闭包。A²⁰⁰⁶中为1的元素个数就是所有从顶点i到顶点j存在一条路径的有序顶点对(i, j)的数目。

Problem F: Strange Way to Express Integers

Suppose C ≡ A₁ (mod B₁) and C ≡ A₂ (mod B₂). Let C = A₁ + X₁B₁, we get X₁B₁ ≡ A₂ − A₁ (mod B₂). Find X₁ using the extended Euclidean algorithm and thus find C. Let B = lcm(B₁, B₂), then the two equations above can be replaced by C’ ≡ C (mod B). Iterate until there is only one equation.

假设C ≡ A₁ (mod B₁)，C ≡ A₂ (mod B₂)。令C = A₁ + X₁B，那么X₁B₁ ≡ A₂ − A₁ (mod B₂)。用扩展欧几里德算法求出X₁，也就求出C。令B = lcm(B₁, B₂)，那么上面两条方程就可以被C’ ≡ C (mod B)代替。迭代直到只剩下一条方程。

Problem G: Tunnel Warfare

Denote the unattacked or rebuilt villages with 0 and destroyed villages with 1, then the problem is reduced to finding the first 1’s to the left and to the right of some element in a string of 0’s and 1’s. Using a binary search tree or dividing the string into segments as long as the square root of the length of the string will solve the problem. Taking advantage of the condition that reconstruction was done in the reverse order of destruction, using a binary indexed tree will also do.

用0表示没有受到攻击或者已经重建的村庄，用1表示被摧毁的村庄，那么问题就规约为寻找一个01序列中某个元素左边和右边的第一个1。用一个二叉搜索树或者将串切分成长度的平方根那么长的小段都可以解决这个问题。利用按摧毁的逆序重建的条件，用树状数组也可以解决这个问题。

Problem H: M × N Puzzle

If N is even, transpose the puzzle. Write down the numbers on the tiles in both the starting and goal states (0 for the missing tile) in row-major order to form two sequences of integers. Let I₁ and I₂ be the numbers of inversions of the sequences and D be the Manhattan distance from the position of the missing tile in the starting state to that in the goal state. The puzzle is solvable if and only if I₁ + I₂ + D is even.

如果N是偶数，交换行列。将初始状态和目标状态的木块上的数字按行优先顺序写下来变成两个整数序列。令I₁和I₂为它们的逆序数，D为空位在初始状态和目标状态中位置的曼哈顿距离。游戏可解当且仅当I₁ + I₂ + D为偶数。