Problem A: 3-dimensional Musical Water-fence
By real-life experience, the order of operations of pouring water will not affect the amount of water that flows out of the fence. Based on this fact, we can process the operations in any specific order. A clever choice of the order can greatly facilitate the simulation. In our reference solution, that order is the decreasing order by the highest levels water can reach above the squares which operations pour water upon. To further simplify the situation, contiguous squares with the same such highest levels can be grouped together. Then simulation starts, following the aforementioned order. Whenever any water flows out of the fence, it is accumulated so that the final answer is found.
Problem B: Clever Y
This is essentially the problem of discrete logarithm. No efficient algorithm is known. The author suggests the following method. For the congruence equation XY ≡ K (mod Z), let L be some specially chosen constant, rewrite XY as XY = XuL · Xv, where Y = uL + v (u, v ≥ 0, v < L). For each u = 0, 1, …, we try to determine whether there exists some v that satisfies the equation. And this is where the very hard part of the method lies. Let A = XuL and B = Xv, then equation is reduced to AB ≡ K (mod Z). All possible values of B will be of the form pZ0 + q (0 ≤ q < Z0), where Z0 is some divisor of Z. Therefore we can build a table to store the values of Xv mod Z0 for every possible v and Z0 and use table look-ups to find the value of v.
Problem C: Difference between Triplets
The following identity gives the essential idea of the solution:
With that, we can apply mapping f : (I, J, K) → (I − J, J − K, K − I). Then the three components of the triplets will get separated.
Problem D: Sequence Partitioning
Performing bisection on the answer will reduce the problem to a new one that requires only to determine the feasibility of the value we guess, which is a little bit easier. The new problem can be solved using dynamic programming. We begin with a O(N2) time algorithm, which is obviously too slow. However, it can be optimized by reducing repeated computations and using subtle data structures to run in O(N log N) time.
Problem E: Game
Only points lying on the convex hull of all points are of interest. Each time we remove a point and fix the hull. Only the “damaged” portion of the hull has to be recomputed. The total time needed for all computations can be linear in a good implementation.
Problem F: Robots
Each rotation can be represented by a square matrix. The combination of multiple rotations can be represented by the product of the rotations’ corresponding matrices. Since rotations are always applied to a contiguous portion of joints, segment trees can be used to speed up the algorithm.
Problem G: Soldier
If we rotate the chessboard by an angle of 45 degrees, the squares that a soldier controls will form a big square. Coloring the chessboard with two colors as in the following figure
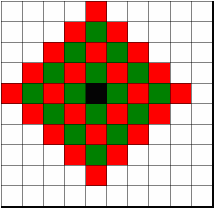
will show that squares of different colors being counted separately would make things simpler. Thus the problem is reduced to find the total area covered by multiple squares. But the existence of chessboard boundaries introduces some trouble. Therefore we employ an indirect approach. First all squares are counted with the boundaries neglected. Then squares lying outside the boundaries are counted. The difference of these two counts will be the answer. Finding the former count is easier. What is shown below presents a way to find the second count.
Assume we can count squares lying in some half-plane or quarter-plane. We make use of this relation:
A + B + C + D + E + F + H
= (A + B + C) + (A + D + F) + (C + E + H) + (F + G + H) − A − C − F − H.
Problem H: Test for Job
We can use dynamic programming to find the longest path in a directed acyclic graph in linear time.
