Autumn is a Genius
这个是本次比赛中最简单的题目,求两个数的和。不过本题中有一个需要注意的地方,就是题目中说了 A , B 是整数且不超过 32767. 但是没有说 A, B >= 0 。所以 A , B 可能是一个绝对值非常大的负数。那么这就是一个简单的高精度加 / 减法问题了 :)
Beautiful Numbers
题目描述为找到 B 进制表示下前 N 个数字和能被 B 整除的正整数的总和。注意,这里是在 B 进制下数字和可以被 B 整除。这就意味着存在下面的重要性质:
对于 B 进制下的一个正整数,如果我们先不考虑最低位 ( 也就 xxxx? 这种形式 ) ,对于较高几位被确定的一个数,我们可以找到唯一 ( 且必然存在 ) 的一个数字,将其放在最低位,使得数字和被 B 整除。
为什么呢?因为前若干位的数字和加起来除以 B 的余数肯定是 0 到 B - 1 的一个,而我们这里使用的恰好是 B 进制,刚好可以用 0 到 B - 1 的数字。所以我们可以找到一个唯一的对应将其填成数字和为 B 倍数的 "Beautiful Number" 。 (0 对应 0 , 1 对应 (B-1) , 2 对应 (B-2) .... )
那么这样一来,算法的轮廓就出来了。我们找到的前 N 个数 , 如果把最低位扔掉,必然是 1,2,3...N 。那么不管最低位,总和应该为 Sum( 1 .. N ) * B ( *B 是因为我们把最低位扔掉了 )
所以接下来我们的目标就集中在如何计算最后一位上面。题目中要求 " 正整数 " 这会使得规律比较难以被发现 . 其实如果我们把 0 也算进去 (0 显然是 "Beautiful Number") ,末尾的变化是很有规律的 , 从 0 开始 , 每连续的 B 个数 , 肯定是 (0 到 B-1) 各出现一次 ( 这个很容易证明,因为我们是在 B 进制下 !!) 。那么从 0 开始每连续 B 个整数的末位和就是 Sum (0 .. B-1) 。所以我们需要计算的只有剩下的不超过 B 个。那几个就直接 Log(B , N) 分解,计算末位即可。所以总时间复杂度为 O(B * LogN * 高精度计算常数 ) 。
* 以上 Sum(a..b) 表示从 a 到 b 求和, Sum(a..b) = (a + b) * (b - a + 1) / 2
Checking the Text
这道题目的意思就是给定一个串,要求支持两种操作:插入单个字符或者询问从两个位置开始的最大匹配长度。为便于讨论,我们认为串初始长度为 L ,插入命令有 A 个,询问命令有 B 个。
如果没有插入操作,就是经典的 LCP 问题,可以用后缀数组在 O(LlogL) - O(1) 的时间内解决(假定后缀排序需要 O(LlogL) 时间)。但是我们现在加入了插入命令,又该怎么做呢?在每次插入之后重新做一次后缀排序似乎是可以的,复杂度为 O(ALlogL) ,但后缀排序常数因子较大,实际效果比想象中差得多。标准解法是对原始文本进行一次后缀排序,预处理出所有的 LCP 询问。当有新字符插入时,将其看作插入到原文本的“空隙”中。对于某次询问命令,首先比较从 i 和 j 开始的连续一段“空隙”中没有字符的文本的 LCP ,遇到“空隙”中的字符再逐个比较。这样对于每次询问命令,比较单个字符的次数不会超过 O(A) 次,计算 LCP 的次数也不超过 A 次。因此总时间复杂度就是 O(LlogL+AL+AB) 。Distributing tasks
本题给定一个 2 * n 的矩阵,矩阵的每个元素都是一个非负整数。要求将其划分成 m 个子矩阵,使得元素和最大的子矩阵元素和最小。
标程算法是二分答案,再用动态规划算出要达到这个答案,至少要划分成几块。以下主要讨论动态规划过程:假设当前枚举的答案是 limit ,矩阵中元素为 a[1..2,1..n] ,另外定义 a[3,i]=a[1,i]+a[2,i] 。用 opt[i] 表示对前 i 列进行划分需要的最少块数,则: opt[i]=min{opt[j]+cost[j+1,i]} ,其中 0<=j<=i-1 ,而 cost[i,j] 表示的是把第 j+1 列到第 i 列划分所需的最小块数。这一段要么划分成一个 2*k 的矩形,要么划分成若干 1*k 的矩形,并且这些矩形之间是无缝的。
具体计算的时候并不是枚举 j ,而是设立两个指针 p,q ,初始时 p=q=i 。每次选择 p 和 q 中较大者尽量往回跑(能跑多远可通过 O(n) 的预处理计算)。然后用跑的次数(也就是分得段数) c+opt[max(p,q)] 来更新 opt[i] 。直到再次出现 p=q 时停止。
这个算法的复杂度是 O(n^2logw) ,但因为 m 较小,实际效果远比这个好。
End of windless days
实际上就是最经典的矩形面积并。但是要注意一点,就是投影范围可能超过了候车室。样例正好误导人忽略这一点。数据范围只有 500 ,怎么做都行,离散化统计或者矩形切割都能 AC 。 我们本来想把这道题目出复杂点,一个是最近比较忙,而且是第一次办比赛,也把握不好难度,所以我们决定第一次就简单一些。
Feed the dogs
本题给定一列数,要求询问 m 个区间中的第 k 小元素,但是这 m 个区间是不会互相包含的。
把 m 个区间按照左端点排序,依次考察每个区间,同时维护一个集合。考察某个区间 [s,t] 时,把在集合中不在区间中的数删除,把不在集合中在区间中的数加入,最后记录集合中的第 k 小值。
由于这 m 个区间互不包含,因此在排序后每个数最多进一次集合,出一次集合。如果我们用平衡树来维护这个集合,那么插入、删除与求第 k 小值的复杂度都是 O(logn) 级别的,总复杂度就是 O(nlogn+mlogn) 。
Going from u to v or from v to u
这是本次比赛中的一个送分题。
题目为:给一个有向图,问是否对于图中任意两点是否从 u 到 v 或者从 v 到 u 都是可达的。最暴力方法为 floyd 求闭包。但这个是很慢的。
首先,可以发现,在一个强连通块内的点互相都是满足要求的,并且将他们压缩为一个点并不影响问题。所以,第一步就是将图中所有的强连通块缩点。那么此时,原图就变成了一个拓扑有序的图。而一个拓扑有序的图中对于任意两点都满足要求以为着什么呢?图中必然存在一条链经过所有点。这个很显然且容易证明。所以第二步就是 DFS 求最长链即可。
时间复杂度 O(n + m)。
Housewife Wind
在阅读本解答之前,您必须知道 LCA 问题、欧拉序列以及线段树。
本题给定一棵带边权的树,要求支持两种操作:询问树中某两点间的距离,修改某条边的权值。假设没有修改操作,就可以直接转化为 LCA 问题解决:令点 1 为根节点,预处理每个点 u 到根节点的距离 dist[u] 。假设询问 u 到 v 的距离,就求出它们的最近公共祖先 par , u 和 v 之间的距离就是 dist[u]+dist[v]-2*dist[par] 。
现在考虑有修改操作的情况。修改一条边的权相当于把某个棵子树中所有的节点到根的距离改变了。对应到 DFS 得到的欧拉序列中,就是把连续一段节点的位置平移了。举个例子来说,假设有一棵树:
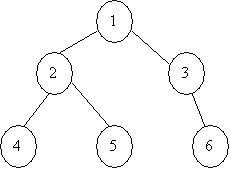
欧拉序列就是 1 2 4 2 5 2 1 3 6 3 1 。如果改变边 1-2 的权值,节点 2,4,5 到根节点的距离就发生了变化。而如下划线所示,它们在欧拉序列中的位置是连续的,位于节点 2 (也就是子树根节点)第一次出现和最后一次出现的区间内。因此只需要把这段区间平移就行。统计某个点 u 到根节点的距离时,只需要用 dist[u]+ 平移量就可以了。对于区间的平移和统计可以用线段树实现,每次操作的复杂度都是 O(logn) ,因此本题复杂度就是 O(nlogn+qlogn) 。