While solving non-linear equations in numerical analysis lesson, professor Busoniya introduce us Newton's Method. Like the other ways (such as bisection, Muller's Method), this method is also based on a linear approximation of the function, but does so using a tangent to the curve. The figure below gives a graphical description.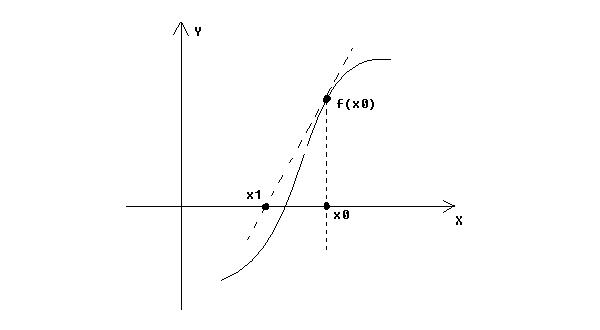

Starting from a single initial estimate, x₀, which is not too far from a root, we move along the tangent to its intersection with the x-axis, and take that as the next approximation x₁. The general term is: x_n+1 = x_n - f(x_n) / f′(x_n), n = 0, 1, 2, .... Newton’s algorithm is widely used because it is more rapidly convergent than any of the methods discussed so far. Then now, you task is to accurate how many iterations it takes to get a root using Newton's Method. The x₀ and the equation are given and all the tolerance is 0.000001. You just use this method to get the answer. The iteration will stop when |x_n+1 - x_n| < tolerance or |f(x_n)| < tolerance then n is the answer. But sometimes the x₀ or equation we choose is so bad that we cannot get the answer using this method within 1000 iterations, then just output "Bad x0 or bad equation!"

There are multiple cases ended by EOF. Each case has two lines, first line is the equation and the second line is x₀. We ensure that each equation just contain integers, 'x', '+', '-', '=' and '^', the right part of '=' is always 0, and there is a space between each term. The number of terms in the equation is less than 50 and all integers in the equations are less than 1000.

For each test case, output n or "Bad x0 or bad equation!" per line.