Still remember those games we played in our childhood? Folding and cutting paper must be among the most popular ones. Clever children will always search for something new, even when they play games like cutting paper. Now, Carol, a smart girl, asks her brother Mike to solve a puzzle. However, as always, Mike cannot find the solution, therefore he turns to you for help.

Carol's puzzle is simple to state. She folds the paper in a certain manner and then uses a knife to cut through the folded paper. What Mike needs to do is to tell how many pieces the folded paper will turn into after it is cut. To eliminate the ambiguity, we can coordinate the paper as [0, 1] * [0, 1], with the coordinates of lower left corner (0, 0). A fold is denoted by two points (x1, y1) and (x2, y2) on the folding line, with which, the direction of the line is determined by from (x1, y1) to (x2, y2). Carol will always fold the paper from left to right relative to the directed line given (see Figure-1). The cut is determined by the two points on the cut line. Please note that the points given to determine the fold or the cut are not necessarily on the paper.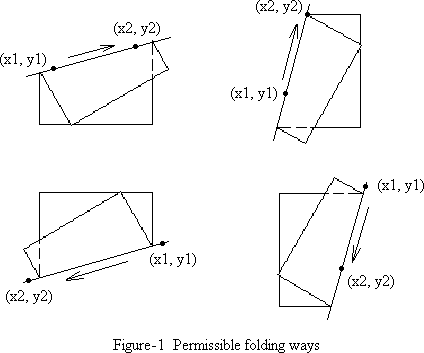

The first line of the input contains one integer t, the number of test cases. Then t cases follow. For each test case, the first line consists of an integer N (0 <= N <= 20), the number of folds, and the following N lines give two points on each fold line as x1, y1, x2, y2. The following line gives two points on the cut line in the same way.

For each test case, output one line containing the number of pieces the paper will turn into after the cut.

2
1
0 0.5 1 1
0.5 0 0.5 1
1
0 0.5 1 1
0 0.4 1 0.4

2
3